1. Multi Layer Perceptron
- 여러개의 결정경계를 학습할수 있는 퍼셉트론
1) Multi-Layer의 구성
(1)다층 퍼셉트론
- 입력층과 출력층 사이에 1개이상의 층이 있는 FeedForward 신경망
- 여러개의 경계를 구성하여 적절한 분류가능

① Hidden Layer
- 은닉층을 이용한 다양한 경계의 표현이 가능
- 내부층의 레이블이 제공되지 않음 ( 관련 학습 알고리즘 필요 )
(2) Back Propagation(역전파)
- 1974년 Paul Werbos, 1986년 Rumelhart등이 발표한 Feedforward신경망의 학습 알고리즘
- Rumelhart의 논문에서는 활성함수로 시그모이드 함수 (모든 u값에 대해 미분값 계산가능)
① Gradient Descent
- 함수의 결과값을 가장 minimum으로 이동하기 위해 gradient descent를 이용해 update
- 함수를 특정 벡터(파라미터)로 미분한 값은 contour와 직교하며, 가장 급격한 경사값
- 여러개의 벡터로 편미분한 결과의 행렬

② 출력층 연결가중치 ( 경사하강법에 의한 Backpropagation )
- 손실함수를 가중치에 대해 미분하여 얻은 Gradient Descent의(-)로 뉴런의 가중치를 update
- Gradient Descent(활성함수(𝝁)를 통해 얻은 추정치와 레이블의 연산결과인 𝜹값*해당 뉴런의 입력)

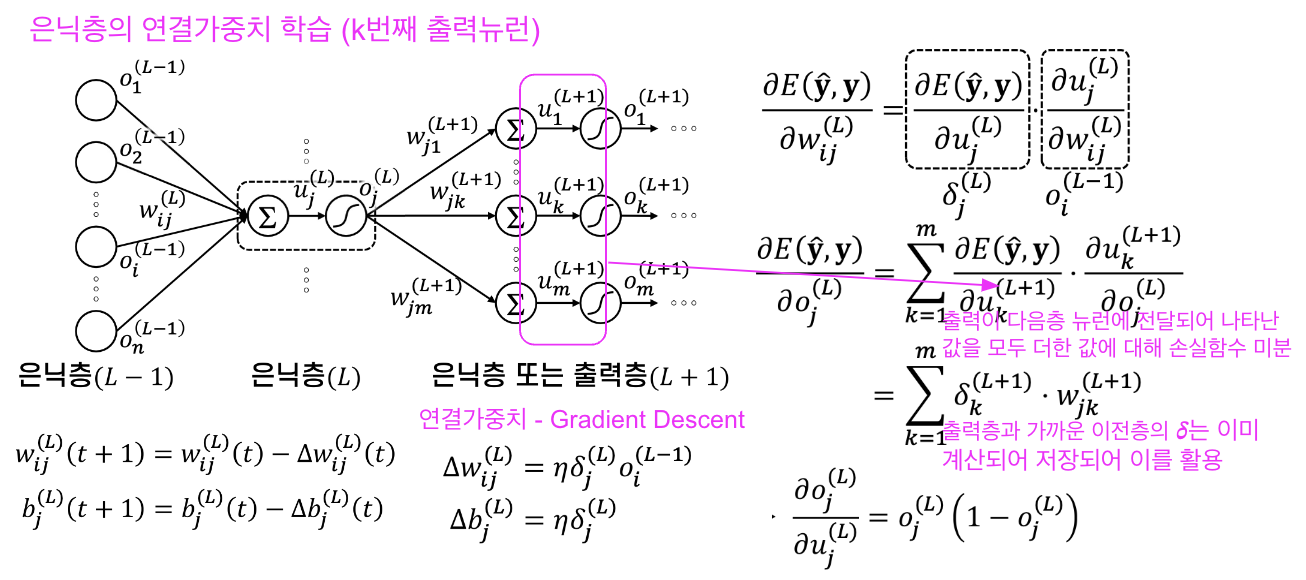
③ 은닉층 연결가중치 ( 경사하강법에 의한 Backpropagation )
- 손실함수를 가중치에 대해 미분하여 얻은 Gradient Descent의(-)로 뉴런의 가중치를 update
- Gradient Descent(출력층에 가까운 층부터 연산되어 이미 저장된 𝜹값*해당 뉴런의 입력)
(3) Momentum
- 가속기법을 이용한 경사하강법의 개선
- 𝝎의 변화량을 속도의 개념으로 보고, 이전 시점의 속도를 일정 비율(m)로 반영

2) 실습
1) Dense층
① variables
self.nIn , self.nOut : 완전연결층의 입력 및 출력
self.w, self.b : 가중치 & bias
self.activation : 활성함수
self.dE_du : ∂E/∂u
slef.do_du : ∂O/∂u계산
self.velocity_w , self.velocity_b : 모멘텀을 적용한 가중치 변화량
self.in_vec, self.out_vec : 역전파를 위한 층의 입력과 출력값 저장변수
② methods
__init__ (self, nIn, nOut, activation='sigmoid', loss='mse') : 완전연결층의 입출력갯수 & 함수
output (self, X) : 입력 X에 대한 출력계산
gd(self, dw, db, momentum = 0) : gradient descent 적용으로 w,b갱신
dE_du_sigmoid_mse(self, y) : 손실함수 MSE일때 적용되는 ∂E/∂u계산
dE_du_sigmoid_ce(self, y) : 손실함수 CE일때 적용되는 ∂E/∂u계산
do_du_sigmoid(self) : 시그모이드 함수에 대한 ∂o/∂u계산
2) BP_Model (역전파 학습을 하는 피드포워드 모델 클래스)
① Instance variables
self.nLaysers: 모델의 층수
self.layers : 모델을 구성하는 완전연결층의 배열
self.ohe : 레이블을 ont-hot encoding한 벡터의 배열(3가지이므로 1,0,0/0,1,0/0,0,1)
self.loss : 손실함수
② methods
__init__ (self, nUnitList, loss='mse' , activation_h='sigmoid' , activation_o='sigmoid')
nUnitList : 층의 입출력 List 예) [2,4,3,1] : 3개층, 2개→4개(1층),4개→3개(1층),3개→1개(1층)
predict(self, X) : 입력 표본 X(배열형태) 에 대한 출력을 추론
fit (self, X, y, N, epochs, eta=0.01, momentum=0 ) : N개의 입력표본배열X와 레이블 y로 모델훈련
2. Multi Layer Perceptron_다중 클래스 분류
- label이 3개 이상으로 주어지는 다중 클래스 분류
1) Multi-Layer와 다중출력의 구성
(1) 다층 퍼셉트론 _ 다중 클래스
- 여러 개의 출력 클래스를 구성하여 가장 확률값이 높은 class로 출력
- 출력은 one-hot encoded label제공
① softmax함수
- 다중 클래스 분류문제에서 출력층의 활성함수로 적합한 함수
- 출력은 클래스 집합의 확률분포를 나타내는 값

② 교차 엔트로피 (cross entropy) _ 손실함수
- 추정된 확률분포와 레이블에 해당되는 확률분포의 차이를 측정하는데 적절한 손실함수
- softmax함수와 함께 사용됨

③ 연결가중치와 최종 출력
- 손실함수를 가중치에 대해 미분하여 얻은 Gradient Descent의(-)로 뉴런의 가중치를 update
- 이전 단계의 𝜹를 이용하여 은닉층의 가중치 조정
- 최종적으로 가장 높은 확률을 나타내는 index의 class로 출력

2) 실습
'스터디 > Deep Learn' 카테고리의 다른 글
| 6. AutoEncoder & GAN , RNN (0) | 2024.09.29 |
|---|---|
| 5. Deep CNN (0) | 2024.09.27 |
| 4. CNN Basic & LeNet5 (0) | 2024.09.27 |
| 3. 프레임 워크와 학습 기술 (0) | 2024.09.25 |
| 1. 인공신경망과 퍼셉트론 (0) | 2024.08.31 |