1. 인공지능 구현

1)인공 신경망
두뇌를 구성하는 생물학적 신경 시스템의 원리를 바탕으로 설계된 계산 시스템
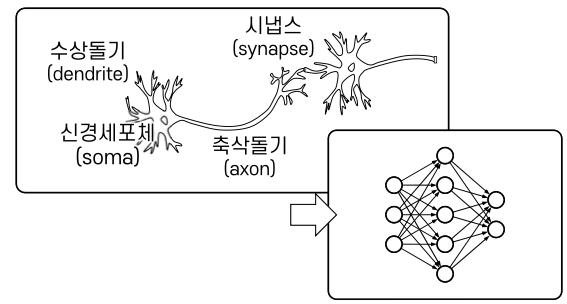
(1) 인공 신경망
초기의 신경망 연구
1943, Warren McCulloch등 : 임계치 논리(threshold logic)알고리즘 바탕의 신경망계산모델 제안
1949, Donald Hebb : 헵의 학습(Hebbian learning)이론제시, 연결의 가중치 조정을 통한 학습
1957, Fank Rosenblatt : Perceptron학습 모델, Mark1 Perceptron구현 (이진 분류기 학습모델)
1969, Marvin Minsky : 퍼셉트론의 한계지적 (XOR문제), 신경망 연구침체
1974, Paul Werbos, 1986, David Rumelhart, 다층 퍼셉트론 학습방법, 역전파 알고리즘
신경망의 층과 표현력
심층 신경망 ( Deep Neural Network) 많은 수의 층으로 구성하면 더욱 높은 차원의 표현이 가능함
Deep Learning 심층 신경망을 학습하기 위해 활용되는 기계학습 알고리즘
- 학습 성능을 제한하는 제반 문제의 개선필요 (부족한 학습 데이터, 불안정한 경사, 과적합, 방대한 계산량)

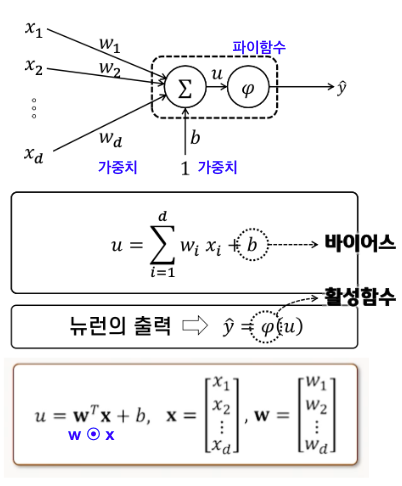
(2) 인공 뉴런
활성함수 (activation function) 𝝋(𝑢)
일반적으로 비선형 특성을 가지는 함수를 사용
𝑢의 값이 0보다 작으면 출력을 억제하고, 0보다 크면 출력을 내도록 설계
바이어스(bias)
뉴런이 활성화되는 𝝎ᵀх의 레벨을 조정
(3) 활성 함수
① Step function
- 정의역을 유한한 개수의 구간으로 나누어 각 구간에서 상수인 함수
- 단위계단함수 (unit step function, Heaviside step function)
② Sigmoid Function
- S자 곡선 형태의 함수, 로지스틱(통상 시그모이드라 불림), 쌍곡탄젠트 (tanh), 오차함수(erf)등
- 모든 u에 대해 미분가능, '경사소멸'문제
③ ReLU 함수
- 심층망에서 경사소멸 문제를 개선하기 위해 시그모이드의 대안으로 활용되는 활성함수
- u=0에서는 미분 불가, Dying ReLU의 문제 ( u<0보다 작으면 0이 되어, 이후 어떠한 값에도 출력없음)
④ ReLU변형 - Leaky ReLU, PaRameteric ReLU, GELU, Swish

(4) Feed-Forward Neural Network
입력층에서 출력층 방향으로 뉴런층의 연결이 이루어지는 구조
① Single Layer Perceptron
: 하나의 층으로 구성된 가장 기본적인 Feedforward 신경망 구조, step function사용

→ 하나의 선형결계가 아닌 것의 학습은 어려움
→ 단위계단함수는 0또는 1의 출력으로 학습표본에 대한 분류가 맞다면 오차 𝜹으로 0이면 파라미터 변화없음
따라서 새로운 데이터에 대해 결과가 적절하지 않을수 있음
- 활성함수를 변경하면 모델학습을 하면 보다 나은 결과를 얻을수 있음
(5) 실습 : 싸이킷런의 Iris데이터를 이용한 single-layer perceptron구현





출력결과 :

'스터디 > Deep Learn' 카테고리의 다른 글
| 6. AutoEncoder & GAN , RNN (0) | 2024.09.29 |
|---|---|
| 5. Deep CNN (0) | 2024.09.27 |
| 4. CNN Basic & LeNet5 (0) | 2024.09.27 |
| 3. 프레임 워크와 학습 기술 (0) | 2024.09.25 |
| 2. MLP (0) | 2024.09.23 |