개발시작

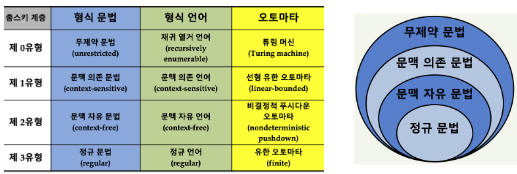
1. 오토마타 오토마타 스스로 움직이는 기계, 컴퓨터 : 유한상태 오토마타 튜링머신 (Turing machine) 메모리테이프, 헤드, 상태기록 레지스터, 유한테이블 (명세된 명령어, 별도의 인풋은 없음) 형식언어 프로그래밍 언어들의 일반적인 특성을 추상화한 개념, 형식문법 프로그래밍 언어의 생성규칙을 추상화한 개념 촘스키 계층 (1) 유한 오토마타 (2) 결정적 유한 오토마타 (deterministic) FA 출력기호와 출력함수가 없으며 수락상태가 있는 오토마타 (3) 비결정적 유한 오토마타 (nondeterministic) FA 입력이 없는 경우 상태를 전이하는 오토마타 ( ε 전이 : 입력없이 상태를 전이 ) 2. 마르코프 연쇄 (1) 마르코프 연쇄 마르코프 성질을 만족하는 이산확률과정 유한 오토마..

Discrete Mathematics 1. 약수와 배수 (1) 나눗셈 a는 정수이고 b는 양의 정수라 할때, 다음을 만족하는 유일한 정수 q,r이 존재한다. a = bq +r ( 단, 0 ≤ r < b) (2) 정의 a,b가 정수이고 a≠0 일때, b=ac를 만족시키는 정수 c가 있다면 "a가 b를 나머지없이 나눈다." 또는 "a는 b를 정제한다" 또는 "b는 a로 나누어 떨어진다"고 표현한다. a는 b의 약수 또는 인수, b는 a의 배수라고 하며 기호 a|b로 나타난다. a가 b를 나누지 않을때에는 a∤b (3) 최대공약수 (greatest common divisor) 2. 나머지 연산 (1)모듈로 합동 정수 n과 양의 정수 m에 대해 n을 m으로 나누었을때 나머지를 구하는 함수를 나머지 함수(modu..

1. 기본계수법칙 (1) 곱의 법칙 두사건 A,B가 일어날 경우의 수 N(A) = m, N(B) =n 동시발생확률 N(A X B) = m x n (2) 합의 법칙 두사건 A,B가 N(A) = m, N(B) =n 이고 A ∩ B = Ø, N(AUB) = m+n 2. Permutation (순열) (1)순열 0 ≤ r ≤ n을 만족하는 정수 n,r에 대하여 n개의 원소를 갖는 집합에서 순서를 고려해서 r개의 원소를 뽑는 경우의 수 (2)중복집합에서의 순열 중복된 원소를 허용하는 중복집합의 크기가 n이고 중복된 원소가 각각 p, q, r개가 있을때 n개 모두를 일렬로 배열하는 경우의 수 (3)중복순열 n개의 원소를 갖는 집합에서 중복을 허용하고, 순서를 고려해서 r개 원소를 뽑는 경우의 수 (4)원순열 n개의..

Tree 1. 트리 사이클이 없는 단순 연결 그래프 Trivial tree : 꼭지점 하나인 트리 Empty tree : 꼭지점이 없는 트리 Forest : 한개 이상의 트리로 구성된 그래프 (1) 루트트리 루트노드 T는 다음 조건을 만족하는 1개 이상의 노드(v₁, v₂, v₃ , ..., vₙ)들의 유한집합 나머지 노드들은 m개의 서로 분리된 집합 T₁, T₂, T₃, ... , Tₘ 으로 나뉘며 T¡는 다시 루트트리가 됨 T₁, T₂, T₃, ... , Tₘ 을 각각 v1의 서브트리 (2)트리의 표현 중첩된 집합, 결각, 중첩된 괄호 (3)닮은 트리 구조는 동일하지만, 노드의 데이터 내용이 서로 다른 경우 닮았다고 함 (4)주요 정리 ▷ n개의 꼭지점을 가진 연결그래프가 n-1개의 변을 가지면 해당..

Graph 1. 용어 (1) 그래프는 vertex와 edge로 구성 G = (V, E) (2) 변은 두 꼭지점을 연결(두 꼭지점은 변에 의해 발생) (3) 연결된 꼭지점은 서로 인접 (4) 병렬변 두 꼭지점을 연결하는 변이 복수개 (5) 루프 동일한 꼭지점을 연결한 변 (6) 고립된 꼭지점 어떤 변도 연결되지 않은 꼭지점 (7) 차수 G의 총차수 (모든 꼭지점의 차수의 합 ), v의 차수 (인접한 변의 갯수) (8) Handshaking Lemma 그래프의 총차수는 짝수 (변은 반드시 두개의 끝점) 2. 그래프의 종류 (1) 방향그래프는 변이 방향을 가지며, 무향그래프는 방향이 없음 (2) 단순그래프는 루프가 없고, 병렬변을 가지지 않는 그래프 (반대: 다중그래프) (3) 부분 그래프 그래프의 일부분 (..

Function (1) 함수의 정의 X,Y의 집합에서 X에서 Y로의 함수 f는 ∀x X, ヨ!y ∈ Y, (x,y) ∈ Y, (x,y) ∈ f X에서 Y로의 관계 | f ⊂ X x Y | ( X는 f의 domain(정의역), Y는 공역, y는 x의 상, x는 y의 역상 ) f(X) = { y ∈ Y | ∀x ∈ X , y =f(x)} , 치역 ** ヨ! : there eixsts only one, 곱집합의 부분집합 ▶ 상수함수 f : X → Y, ∀x ∈ X, f(x) = c (c는 상수) ▶ 항등함수 f : X → X, ∀x ∈ X, f(x) = x , Ix ▶ 전사함수 f : X → Y, ∀y ∈ Y, ヨx ∈ x, f(x) = y (치역이 공역) ▶ 단사함수 ∀x1, ∀x2 ∈ X, f(x1) = ..

집합 (Set) 우리의 직관이나 사고로부터 한정적이고 분리된 객체들의 전체 M에서의 수집 1. 집합 무정의 용어 정의없이 사용하는 용어, 직관적으로 이해할수 있으나 다른 용어로 정의하기 힘든 대상을 표현하기 위해 사용됨 (1) 집합의 표기 ▷ S가 하나의 집합이고 a가 집합의 원소이고, b는 집합의 원소가 아니라고 할때, a ∈ S, b∉ S ▷ { }로 표시함 : 원소 나열법, 조건 나열법 S= { 1, 2, 3 }, S= { x | 0 < x < 4 인 자연수 } ▷ 집합의 크기 | S | , | S |= 3 ▷ 집합내에 집합가능, 원소중복 불가 (2) 부분집합 ▷ 부분집합 (공집합 포함) A의 모든 원소가 B의 원소이면 A는 B의 부분집합, A ⊆ B 혹은 A ⊂ B, ∀x ( x ∈ A → x ∈..

이산 수학 ( Discrete Mathmatics) 불연속적인 상태에 대한 수학 ▶ 도구 - 정의, 정리 ▶기법 - 대입법, 가감법, 가우스 소거법(일차 연립방정식), 근의 공식 ▶방법론 - 상황에 따라 가장 효과적이고 효율적인 도구와 기법을 선택 (추상화, 수학적 모델링, 정보 모델링) (1) 추상화 일정한 인식목표를 추구하기 위하여 표상이나 개념에서 특정한 특성이나 속성을 빼냄 문제와 관련된 핵심내용만 남기고 관련없는 내용을 제거하여 단순화시키는 과정 (2) 알고리즘 - 어떤 문제를 해결하기 위한 여러 동작들의 유한한 모임 ▶ computer programming language 세밀하나 핵심요소가 드러나지 않고 부차적인 표현이 많으며 통일된 언어가 없음 ▶ flow chart 알고리즘의 작동방식 도..