1. 강화학습
강화학습 : 출력값에 대한 교사신호가 '보상'형태로 제공, 정확한 값이 아니며 즉시 주어지지 않음
- 제어 문제를 표현하고 해결하는 방법으로 주로 사용
주어진 상황이나 조건에서 어떤 동작을 취해야 할지 결정하는 문제
시간에 따른 순차적인 개념존재, 이전 상황이 현재시점에서의 결정에 영향을 미침
- 주어진 상황에서 최적의 제어신호에 대한 정확한 목표값을 모름
- 제어 동작후 결과에 대한 성공여부 평가는 가능
예) Google DeepMind , AlphaGo ( 몬테카를로 트리탐색, 딥러닝, 강화학습 기술의 결합 )
AlphaGo Zero ( 바둑규칙만 입력, 스스로 대국을 통해 터득 ),
AlphaZero ( 모든 보드게임을 위한 알파고 제로의 범용 버전 )
응용분야 : 보드게임, 비디오 게임, 로봇제어, 시스템 제어
- 게임 분야 : 아타리 게임에 DQN적용
- 로봇 제어 : 모방학습 (비디오 이미지를 보고 로봇이 흉내내서 동작을 배우도록 학습)
- 시스템 설정/제어 : 구글 데이터센터의 Cooling System (구글 딥마인드 강화학습)
외 자동차의 자율주행

1) 강화 학습
① 출력값에 대한 교사신호가 '보상'의 형태로 제공
- 목표 출력값 없음 ( 최종 목표를 지정하고 매순간 학습시스템이 취하는 행동의 결과에 따라 보상제공)
② 목적
- 최종적으로 얻게되는 누적보상의 최대화 ( 목표달성에 적절한 경우 양의보상, 부적절한 경우 음의보상 )
- 보상을 통해 좋은/나쁜 행동을 배워 행동방식을 긍정적 방향으로 '강화'
- 보상의 주체 : 에이전트와 환경 (환경이 보상을 결정하고, 에이전트가 결정을 집행)

(1) 마르코프 결정 프로세스 : S,A,R,P, 𝜸 , 𝝅 , Gₜ
- 현재 상태에서 다음 행동을 선택할때 이전 선택들의 영향이 없이 현재 상태에 의해서만 결정
① MDP, Markov Decision Process
학습을 위해 에이전트 - 환경의 상호작용을 수학적으로 표현한것
정책 - 에이전트가 정책에 따라 행동을 결정할때 사용하는 규칙, 에이전트는 정책에 따라 행동을
결정하고, 환경은 주어진 MDP에 따라 다음 상태와 보상을 결정
목적 - 주어진 MDP내에서 누적보상을 최대화하는 최적의 행동을 결정하는 정책을 찾는것
마르코프 성질 - 다음 행동은 현재의 상태(상황)에 의해서만 결정
② 마르코프 프로세스는 <S,A,R,P, 𝜸 >의 튜플 (상태, 행동, 전이확률, 보상함수, 보상의 할인율)
S - 가능한 상태의 유한집합
A - 가능한 행동의 유한집합
P - 상태 전이확률

R - 보상함수

𝜸 - 보상을 계산할때 사용되는 할인율 𝜸 ∈ [0,1] (목표와 먼 결정은 보상의 기여도 낮음)

(2) MDP 정책과 가치함수
① 정책 𝝅 : 상태 𝐒ₜ와 행동𝐀ₜ의 시퀀스를 결정하는 함수적 규칙
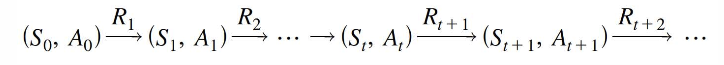
𝝅 ( a | s ) = P [ 𝐀ₜ = a | 𝐒ₜ = s ] , 주어진 상태가 s일때 a를 선택할 확률

② 좋은 정책에 대한 평가기준 필요
수익 return, 이익 grain Gₜ , 시점 t에서 얻어지는 보상에 대해 할인율 𝜸을 곱하여 더한값 (총할인 보상)
( 𝜸는 시점이 멀어질수록 Gₜ 에 기여도 낮게 설정 ), 모든 시점에서의 보상에 할인율을 반영, 이익산정

- 가치함수
학습의 목적 : 최종누적보상을 최대화하는 최적 정책(optimal policy) 𝝅* : S ↦ A를 찾은것
최적 정책을 찾는 방법 : 상태와 행동에 대한 가치 평가를 수행
상태가치함수 : 상태 s에서 정책 𝝅에 따라 행동하였을때 얻을수 있는 기대보상 (보상의 평균)
행동가치함수 : 상태 s에서 정책 𝝅에 따라 행동 a를 선택하였을때의 기대보상

- 최적가치함수

- 최적정책 : 최적행동 가치함수 q*(s,a)를 최대화하는 행동을 찾는것

(3) 최적 정책을 찾는 과정의 어려움 ( MDP 학습 )
- 에이전트는 상태와 보상에 관해 오직 지역적/부분적 정보만 이용가능
(현실적으로 모든 경우의 수를 다 계산해볼수 없음)
- 보상이 즉시 주어지기보다는 긴 시간 동안의 지연발생
- 상태 전이와 보상이 비결정론적인 경우, 함수식으로 정해지지 않거나 알려지지 않은 경우도 존재
- 상태공간과 정책공간이 방대
- 비효율적 학습
⇨ 심층 Q-학습이 (Deep Q-learning) 좋은 해결책
2) Q-학습
(1) Q함수 (Q function)

- Q값 (Q value) : 주어진 상태-행동 쌍의 기대보상 Q함수의 값
- Q학습 (Q learning) : 최적정책 𝝅*를 얻기 위해 최적 Q함수 Q*(s,a)를 추정하는 방법
- Q학습 알고리즘 :
초기화 ▶ 임의의 현재상태 s 지정 ▶ 다음 행동 a 선택으로 s'로 이동 보상 r획득
▶ 상태 s'와 보상 r로 Q갱신 ( Q함수의 추정치는 s'에서 얻어지는 모든 행동 중 최대값으로)
▶ 상태변경 및 보상, Q갱신을 반복

예) 미로찾기 학습의 예

(2) 행동 선택을 위한 전략 : 탐험과 탐사
탐험 : 탐색공간 전체를 골고루 찾음, 랜덤하게 다른 행동을 선택
탐사 : 특정한 곳을 중심으로 주변을 집중적으로 탐색 (현재의 Q함수 정보를 바탕으로 최적의 행동 선택)
혼합된 선택전략 ε-greedy (엡실론 탐욕)

ε : 탐험 확률, t가 커지면서 점점 감소 ( 시간의 경과에 따라 탐험감소, 탐사증가 )
(3) 경로 선택
- 여러 경로중 짧은 경로를 설정하기 위해 할인된 미래보상 개념도입
(Gt - 미래에 얻어질 보상에 대해 할인율 적용)
예) 더 나은 경로 선택 (할인율 적용)

(4) 비결정론적 환경
결정론적 모델 : 모델의 출력과 행동이 어떤 임의성도 없이 초기조건과 파라미터에 의해서만 전적으로 결정
확률적 불확실성이 존재하지 않음
비결정론적 모델 : 모델에 임의성이 내재, 동일한 초기조건과 파라미터 집합이어도 서로 다른 여러 출력생성
상태전이와 Q-학습이 제대로 동작하지 않음 , 해결책으로 신뢰요소(belief factor 𝛂) 도입
예) 바둑, 장기, 체스 등 상대방이 있는 경우
𝛂를 가진 Q학습의 갱신 : Q-신경망

➡ Q함수를 Q테이블로 표현시 매우 거대하며 실제 응용시 비효율적이므로 신경망으로 표현,추정시도

3) Q신경망과 Q-심층 신경망 (신경망을 이용하여 Q-함수 추정 )
(1) Q신경망 : Q함수를 테이블이 아닌 근사함수의 형태로 하여 신경망을 이용해서 표현/추정
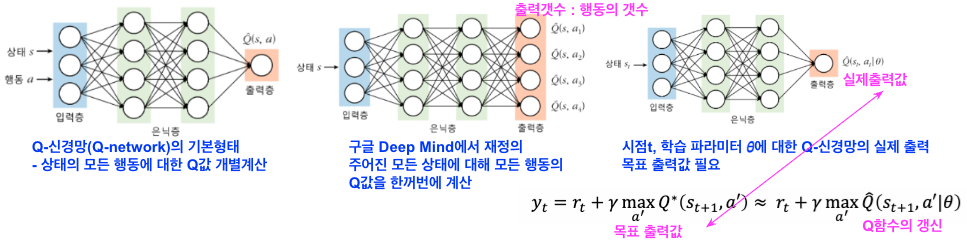
① Q신경망의 두가지 형태
- 상태 s와 행동 a가 주어지고 동작한 경우 기대보상 Q(s,a)
- 입력상태 s만 주어지고 출력층은 주어진 상태의 각 행동에 대한 Q값으로 구성되는 형태
▶ 학습의 불완전성으로 인해 수렴이 보장되지않아 DQN 개발
② 목적 함수 : 오류역파의 지도학습
- 오차제곱합 함수 : 목표 출력값 (Q함수의 최적값 추정치)와 실제출력 비교
- 강화학습에서 최적의 정책을 구하기 위한 Q함수를 구하기 위한 Q신경망이 사용
Q신경망에는 EBP(Error Back Propagation)을 사용하는 지도학습 수행

(2) Q-신경망 학습의 불안정성
① Q테이블 표현에 대해서는 수렴, Q신경망은 발산
② 불안정성의 원인
- 데이터간의 높은 상관관계 : 시간흐름에 따라 순차적인 데이터수집된 데이터를 입력으로 활용
- 목표출력이 시간에 따라 변함 : 평균제곱오차는 Q(목적함수)를 사용하므로 의존성
학습 과정중에 목적함수가 변동
(3) (Deep Q-Network) : Q신경망 학습의 대책
- 심층 신경망: 합성곱 신경망(CNN)구조
영상 픽셀 데이터를 입력으로 미래보상을 추정하는 행동가치함수의 근사함수
- 경험재현(experience replay), 목표망(target network)
① 학습절차 : 2개의 convolution층과 2개의 완전연결층으로 구성
입력층 (128컬러의 210x160 영상을 4개 프레임을 110 x84의 그레이로 축소 후 84x84로 잘라 사용
▶ 1번째 convolution층 (ReLU) ▶ 2번째 convolution층 (ReLU) ▶ 1번째 완전연결층(ReLU)
▶ 선형의 완전연결층 ▶ 출력층 (18가지 조이스틱 조작에 대응한 Q)
** 이후 3번째 convolution층 도입
경험재현 - 데이터간의 높은 상관관계 문제 해결, 재현을 통해 학습 데이터의 시퀀스를 재구성
에이전트의 경험 (sₜ, aₜ , rₜ, sₜ₊₁ )을 시간 간격단위로 재현 메모리 D에 저장 후,
D로부터 균등 무작위 추출을 통해 미니배치를 구성하여 학습진행
예) MNIST데이터의 경우 1을 전부 학습, 2학습하는 방식으로 하면 학습이 잘 되지 않음
데이터간 상관관계가 높음, Shuffle로 데이터를 섞어 미니배치로 학습
목표망 - Q신경망과 별도로 함수 계산을 위한 목표망을 별도로 사용
시변적인 목표 출력값의 문제해결 (목표 출력이 계속변함)
원래의 Q-신경망과 같은 구조이나, 다른 파라미터의 𝜃⁻ 를 가진 별도의 신경망
( 목표망의 파라미터 𝜃⁻가 매 C단계 마다 𝜃을 갱신하여 목표 출력값이 움직이지 않도록 함)



예) 아타리 게임

'스터디 > Machine Learn' 카테고리의 다른 글
| 6. Deep Learning (0) | 2024.08.28 |
|---|---|
| 5. 신경망 (0) | 2024.08.27 |
| 4. 앙상블, 결정트리, 랜덤포레스트, SVM/커널 (0) | 2024.08.20 |
| 3. 비지도 학습_ 군집화와 특징추출 (0) | 2024.08.19 |
| 2. 지도학습- 분류와 회귀 (0) | 2024.08.01 |