1. 군집화
군집화 : 비지도 학습 (클래스 레이블에 대한 정보 없음)
- 데이터 집합의 분포특성을 분석, 서로 교차하지 않는 복수개 부분집합(cluster)로 나누는 문제
내재된 특성과 규칙을 스스로 파악하여, 다음 단계의 데이터 분석을 위한 세로운 정보를 탐색
입력데이터에서 추출된 특징공간에서 특징값의 유사성에 따른 데이터들끼리의 묶음
결과 표현 : Sample(부분집합의), 대표벡터 집합(클러스터의 데이터 평균), 확률분포(평균, 공분산)
활용 분야 : 데이터에 대한 클래스 레이블이 주어지지 않거나 클래스 레이블링에 비용이 많이 드는 경우
1) K-means Clustering ( K-평균 군집화 )
- 주어진 데이터집합을 K개의 그룹으로 묶는 알고리즘
예) 이미지의 경우 배경과 이미지의 그룹화 등에 사용되기 쉬움
(1) 수행단계
시작(초기화) ▶ 데이터 그루핑 ▶ 대표벡터 수정 ▶ 반복 여부결정
① 시작(초기화) : 데이터 집합 { 𝑥₁,𝑥₂,...,𝑥ₙ }에서 임의 K개 선택, 대표벡터집합 생성 { 𝑚₁ ,𝑚₂ ,...,𝑚к }
② 데이터 그룹핑 : 거리 기준으로 데이터들을 K개의 클러스터 분류
k개의 대표벡터와의 거리계산 후 가장 가까운 클러스터로 레이블링

③ 대표벡터 수정 : 그루핑된 각 클러스터의 대표벡터 갱신
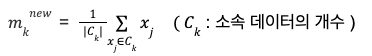
④ 반복여부 결정 : 갱신전/후 대표벡터의 차이를 계산하여 그 값에 변화가 없거나, 설정한 반복횟수까지 반복
(2) 실제문제에 적용시 고려해야 할 사항 검증
- 대표벡터 계산과 Grouping 알고리즘 반복을 수행으로 좋은 군집을 탐색을 보장
- 성능평가 기준이 뚜렷하지 않으므로 목적함수를 정의하여 평가
① 목적함수 J
J (각 클러스터내의 분산을 모두 더한 값) : 값이 작으면 모여있고, 값이 크면 흩어져 있다는 의미
대표벡터와 데이터(클러스터 레이블)로 계산됨, 학습 반복시에 J의 값이 줄어드는 방향으로 학습이 진행
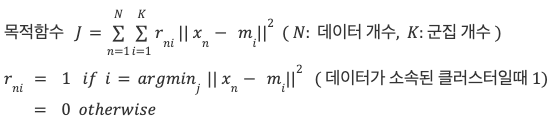
J값을 결정하는 파라미터 : 대표벡터 𝑚ᵢ ( 𝑖 = 1,2,...,K ), 클러스터 레이블 𝑟ₙᵢ에 대해 증명
각 단계별로 최소의 파라미터를 찾고 J값의 변화가 없으면 극소점

→ K-평균 군집화 알고리즘은 목적함수 J를 최소화하는 지역 극소점을 찾는 것을 보장
② 초기대표벡터의 설정이 군집화의 성능에 영향
- 초기 벡터의 설정에 따라 최종적으로 찾아지는 해가 달라짐
데이터에 의존하는 적절한 K값 선택은 문제에 의존적, 다양한 K값에 대해 군집화결과를 비교하여 선택
→ 계층적 군집화를 통해 적절한 K값 선택을 모색
2) Hierachical Clustering ( 계층적 군집화 )
전체 데이터를 몇개의 배타적인 그룹으로 나누지 않고, 큰 군집이 작은 군집을 포함하는 형태로
계층을 이루도록 군집화하여 구조를 살펴보는 방법
(1)병합적 방법과 분할적 방법
병합적 방법 (agglomerative or bottom up) : 각 데이터가 하나의 군집을 이루는 최소군집으로 시작해
단계적으로 병합하여 더 큰 군집을 생성, 모든 데이터를 병합하므로 N-1번의 병합과정 필요
분할적 방법 (divisive or top down) : 모든 데이터가 속하는 최대군집으로 시작하여 특정 기준에 따라
군집을 분할해 나가는 방법 , 가능한 분할방법 2ᴺ⁻¹ -1 개 (비실용적)
(2) 병합적 방법
- 가장 가까운 요소들의 군집을 이루고 점차 병합
- 수행단계 (덴드로그램으로 표현)
데이터 집합 {𝑥₁,𝑥₂,...,𝑥៷}에서 각 데이터가 각각의 군집이 되도록 N개의 군집 {C₁ ,C₂ ,...,C៷}을 설정함
가능한 모든 군집쌍에 대해 군집간의 거리를 계산

거리가 가장 가까운 두 군집 C ᵢ 와 Cⱼ를 선택 병합하여 새로운 클러스터 Cᵢⱼ생성, Cᵢⱼ = Cᵢ ∪ Cⱼ
새로운 Cᵢⱼ를 클러스터 풀에 넣고 기본의 C ᵢ 와 Cⱼ는 제거, 오직 하나의 클러스터가 남을때까지 반복

(2) 계층적 군집화 알고리즘의 특성
군집간의 거리계산방식
최단연결법 (minimum or single linkage) : 가장 가까운 데이터 쌍간의 거리, 고립된 군집을 찾는데 유용
최장연결법 (maximum or complete linkage) : 가장 멀리 떨어진 데이터 쌍간의 거리
응집된 군집을 찾는데 중점 (outlier에 영향을 크게 받음)
중심연결법 (centered linkage) : 두 군집 평균간의 거리, 특이값에 강건함 (outlier에 영향을 받지 않음)
평균연결법 (mean or average linkage): 모든 데이터쌍 간 거리의 평균, 작은 분산을 가지는 군집을 형성
Ward's 방법 : 병합후 클러스터 내부의 분산, 비슷한 크기의 군집을 병합함

덴드로그램으로부터 적합한 군집의 수를 결정하는 방법
- 클러스터간의 거리가 증가하는 동안 클러스터의 수가 늘어나지 않고 일정기간 유지되는 지점선택
------------------------------------------------------------------
2. 특징추출 (PCA, LDA)
- 분석에 불필요한 정보를 제거하고 핵심정보 추출
차원축소를 통한 분석 시스템의 효율향상 (차원의 저주)
x에 변환함수 𝝓를 적용하여 특징벡터 y를 얻음
- 선형변환에 의한 부분공간분석 ( 고차원의 데이터를 저차원에 매핑)
1) 변환함수 (embedding function, transformation function)
① 선형변환 (linear transformation) : 차원 축소를 위해 특정차원에 사영하여 변환
𝑦= Ø(𝑥) = 𝐖 ᵀ𝑥 ( 𝑦가 𝑚 x 1 행렬, 𝑥 : 𝑛 x 1 )
n차원 열벡터 𝑥 에 변환행렬 𝐖( 𝑛 x 𝑚 )곱으로 𝑚차원 특징획득 (x를 𝐖방향으로 사영한 값)
통계적 방법으로 특징벡터 y가 원하는 분포가 되도록 하는 𝐖를 찾음
② 비선형변환 (linear transformation)
𝑦= Ø(𝑥) = 𝐖ᵀ𝑥( 𝑦가 𝑚 x 1 행렬, 𝑥 : 𝑛 x 1 )
복잡한 비선형 함수 Ø(𝑥)를 이용하여 𝑛차원 벡터를 𝑚차원으로 매핑
수작업에 의한 특징추출 (handcrafted)
표현학습 (representation learning)
수작업에 의한 특징 추출 : 입력데이터의 특성과 분석 목적에 맞는 특징을 개발자가 설계함
예) 숫자인식특징 ( 격자특징, 수직히스토그램, 방향특징 등 여러가지 방법을 고려 )
영상분석을 위한 특징 : 에지, 가로/세로 방향성분 분석 등
문서분석을 위한 특징 : 단어의 발생 빈도 등
표현학습 : 특징추출을 위한 비선형 함수를 신경망등의 머신러닝 모델로 표현
학습을 통해 분석이 잘 되도록 변환함수의 최적화가 가능
예) 딥러닝 모델을 이용한 얼굴인식용 특징추출
2) 선형변환에 의한 특징 추출
(1) 차원 축소 관점에서의 특징 추출
주어진 데이터를 변환행렬 𝐖에 의해 정해지는 방향으로 사영하여 저차원 특징값을 얻는것

특징값 𝑦ᵢ는 𝑥를 𝐖의 열벡터 𝑤ᵢ 위로 사영한 값 ( 단,𝑤ᵢ는 unit vector)

예) 2차원의 [2,2]를 𝑤[1,0], 𝑤[2/√5 , 2/√5]로 각각 사영한 결과 , 𝑦 =𝑤ᵀ𝑥

3차원 데이터를 2차원 특징 추출 : 특징값 𝑦ᵢ는 𝑥를 𝐖의 열벡터 𝑤₁,𝑤₂가 이루는 2차원 평면으로 사영한 값
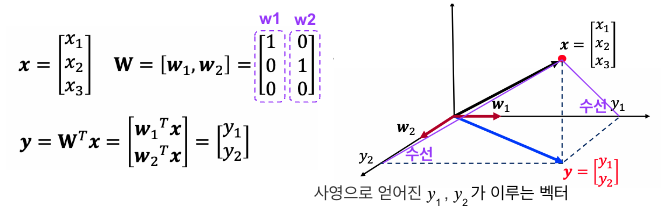
𝑛 차원 데이터의 𝑚차원 특징 추출 : 특징값 𝑦 는 𝑥를 𝐖의 열벡터 𝑤 위로 사영한 값

전체 데이터 집합 에 대한 특징 추출
𝑛 차원 데이터의 𝑚차원 특징 추출 : 특징값 𝑦 는 𝑥를 𝐖의 열벡터 𝑤 위로 사영한 값
𝐗 = { 𝑥₁, 𝑥₂ , ..., 𝑥៷ } ( 𝑛 x N 행렬 )
𝐘 = { 𝑦₁, 𝑦₂, ... , 𝑦៷ } ( 𝑚 x N 행렬 )
𝐘 = 𝐖ᵀ𝐗 = [ 𝐖ᵀ𝑥₁,𝐖ᵀ𝑥₂, ... , 𝐖ᵀ𝑥៷ ]
예) 변환행렬에 따른 특징의 분포 ( 3차원 데이터를 2차원 특징추출 )

좋은 특징추출 : 변환행렬 𝐖를 적절히 조절해서 분석 목적에 맞는 특징 분포를 만드는것
** 통계적 특징 추출은 목적에 맞는 형태로 변환 (분류 목적, 위 그림의 가운데 형태 선택)
(2) 선형변환을 사용하는 대표적인 통계적인 특징추출
주성분 분석법 (PCA) : 비지도 학습 ( 클래스 정보 미사용 )
선형판별분석법 (LDA:Linear Descriminant Analysis) : 지도학습 (클래스 정보 사용)

3) 주성분 분석법 (PCA)
(1)개요
① 저차원으로 하여 특징값 추출하되, 변환 전의 데이터 𝐗가 가지고 있는 정보를 차원축소 후에도 최대한 유지
- 데이터의 집합이 가능한 넓게 퍼질수 있는 방향으로 사영을 수행 ( 분산이 가장 큰 방향으로 선형변환 )
- 가장 큰 분산과 그 방향 = 공분산행렬의 최대 고유치와 고유벡터
② 변환행렬 구성 (W)
데이터의 공분산 행렬의 고유치와 고유벡터를 찾아(eigenvalue decomposition),
고유치가 가장 큰 값부터 순서대로 이에 대응하는 𝑚개의 고유벡터를 찾아서 행렬 𝐖를 구성

(2) PCA의 알고리즘 수행단계
X의 평균과 공분산 계산 ▶ 공분산의 고유치 분석 ▶ 고유치 행렬(대각에 고유치)과 고유벡터행렬(고유
벡터를 열벡터로 가지는 성분)계산 ▶ m개의 고유치 선택 ▶ 열벡터로 변환행렬 생성(크기순) ▶ 선형변환
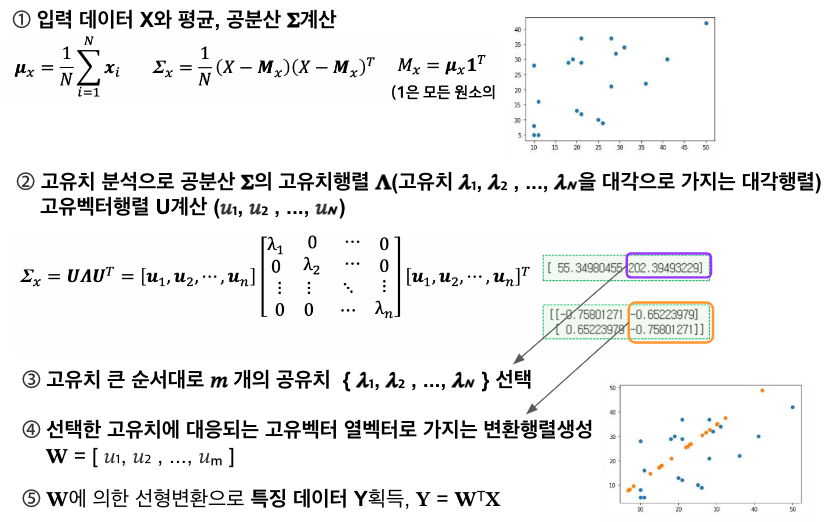
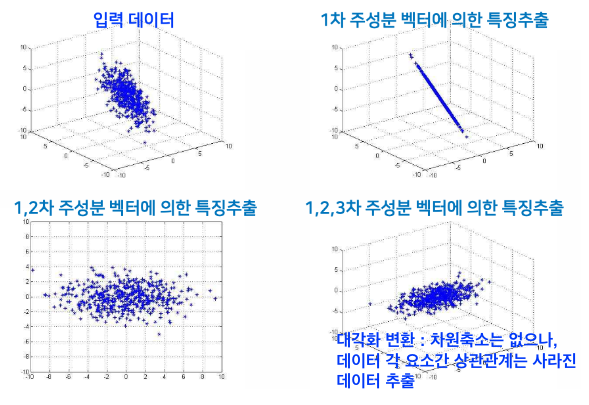
- 차원축소가 없는 경우에도 데이터 요소간 상관관계는 사라진 데이터 추출됨
(3) 축소되는 차원 m
- 차원축소로 인해 발생하는 데이터의 오차를 최소화하는 기저벡터를 탐색하여 수행
( 공분산 행렬의 고유치 분석을 통해 분산이 적은것을 찾아 제거 )
- 저차원 특징 추출을 목적으로 m개의 벡터를 선택사용 (n개 모두 사용시 정보손실없음)
- 정보손실량을 감안하여 m선택 (사전에 사용자에 의해 결정된 역치 θ로 m설정)





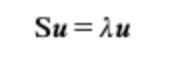

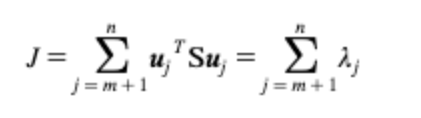
** n차원 입력공간의 경우 임의의 기저벡터 집합 𝑢₁,𝑢₂,..., 𝑢ₙ로 x를 표현
(ㅍ기저벡터가 서로 직교이며 크기가 1(단위직교기저)이라고 가정)
원 벡터와 근사벡터의 차이를 손실정보(J)로 두면 (데이터들의 평균이 0 가정하) S는 공분산 행렬
라그랑쥬 승수(기저벡터가 단위벡터가 된다는 가정만족)로 J 재정의 후 목적함수를 𝑢에 대해 미분
극소(or 극대)지점에서 행렬 S의 고유벡터와 고유치는 기저벡터𝑢와 라그랑스 승수𝝀
-공분산 행렬의 고유치는 해당 고유벡터로 데이터를 사영함으로써 얻어지는 특징의 분산값이며,
정보손실량 J의 최소화는 기저벡터 중 분산이 적은 것을 찾아 제거하여 가능

예) θ = 0.98로 설정하면 손실정보량 2%미만의 m을 찾아 차원을 축소할수 있음
예) 얼굴영상의 표현 ( 𝑛차원을 𝑚차원으로 축소, 𝑛 >> 𝑚 이며 𝑤는 기저벡터 )
좋은 기저벡터 - 'Eigenface' (얼굴 영상에 PCA적용하여 찾아진 고유벡터를 영상으로 표현한 것)
𝑥 = 𝑦𝐖 = 𝑦₁𝑤₁ + 𝑦₂𝑤₂ , ..., 𝑦ₘ𝑤ₘ

(4) PCA의 특성과 문제점
① 특성 : 데이터 분석에 대한 특별한 목적이 없는 경우에 가장 합리적인 차원 축소의 기준
② 단점 : 비지도학습 (클래스 레이블 정보를 활용하지 않음)으로 분류에 핵심이 되는 정보를 손실할수 있음
비선형구조의 분포를 가진 경우 적절한 저차원 특징의 탐색불가
예) 클래스가 있는 정보를 PCA(분산이 큰 방향의 데이터 겹침)분류의 핵심정보 손실초래, 선형변환의 한계
클래스를 반영하여 분류를 하고자 한다면 클래스 정보를 활용한 지도학습 필요 - LDA


4) 선형판별 분석법 (LDA : Linear Discriminant Analysis)
(1) 개요
목적 : 클래스 레이블 정보를 적극 반영, 클래스 간 판별이 잘 되는 방향으로 차원 축소
분류에 적합한 특징의 방향은 각 클래스가 가능한 서로 멀리 떨어질수 있는 거리 유지 (클래스내에서는 응집)
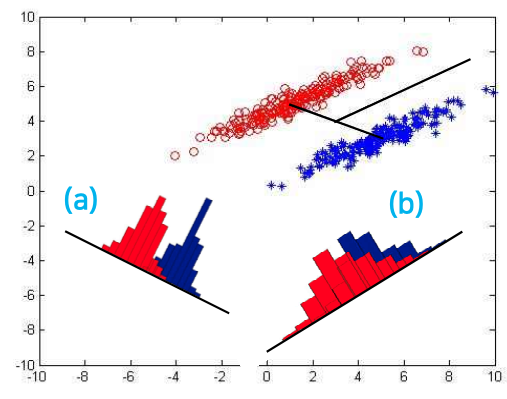
(2) 목적함수
- 클래스 내에서 분산이 적고, 클래스간 분산이 커지도록 함수 설정 (분모: 클래스내 산점행렬)


- 벡터들을 w방향으로 (Ck클래스 내) 정사영하여 얻어지는 평균과 평균 벡터의 w로의 정사영 동일
- sk : 정사영한 후 값에서 평균을 뺀것 (분산에 비례하는 값), s는 클래스 내 산점행렬

5) LDA : 다중 클래스 분류
(1) 목적함수 : 각 클래스 내 산점도는 작게, 클래스간 산점도는 크게
(Trace : 정방행렬의 대각원소의 합을 계산하는 연산)

(2) 알고리즘 수행단계
입력데이터 𝐗를 각 클래스 레이블에 따라 M개의 클래스 분리 ▶ 평균 𝑚ₖ와 클래스간 산점행렬 Sв,
클래스내 산점행렬 Sw계산 ▶ 고유치 분석으로 Sw⁻¹Sв의 고유치 행렬과 고유행렬벡터 계산후
고유치가 가장 큰 순서대로 m개 선택 ▶ 분산 크기로 고유치 m개 선택 ▶변환행렬 생성 ▶선형변환

고유치 분석을 통해 Sw⁻¹Sв의 고유치 행렬 𝚲와 고유행렬벡터 U계산

고유치가 큰것부터 순서대로 𝑚개의 고유치{ 𝝀₁, 𝝀₂ , ..., 𝝀៷ } 선택
선택한 고유치에 대응되는 고유벡터를 열벡터로 가지는 변환행렬 𝐖생성
𝐖 = [ 𝑢₁, 𝑢₂ , ..., 𝑢ₘ ]
𝐖에 의한 선형변환으로 특징 데이터 Y획득, 𝐘 = 𝐖ᵀ𝐗
(6) 선형판별 분석, 장단점
PCA와 LDA
PCA는 공분산 행렬에 대해 고유치분석, 행렬 생성
LDA는 클래스간, 클래스내 산점 행렬에 대해 고유치 분석 , 행렬 생성
장점 : 지도학습 능력
단점 :
- 선형변환의 한계 (복잡한 비선형 구조인경우 적절한 변환불가, 커널법/비선형 매티폴드 학습법이용)
- 선택하는 고유벡터의 갯수(축소된 특징차원) 𝑚의 결정
- 직접 분류를 통해 얻어지는 데이터의 분류율을 기준으로 결정 (여러값을 대입하여 성능시험)
- 행렬 Sw⁻¹Sв를 통해 찾아지는 고유벡터의 갯수 제한(클래스 갯수 M이면 M-1개만 가능)
M개의 클래스의 특징벡터는 최대 M-1차원으로 제한됨
- 작은 표본집합의 문제 (small sample set problem), 클래스내 산점행렬의 역행렬 계산필요
( 입력데이터의 수가 입력차원보다 작은경우 클래스내 산점행렬 Sw의 역행렬이 존재하지 않음)
→ PCA로 차원 축소한 후 이에 대해 LDA적용
6. 거리기반 차원축소 방법
- 선형변환을 통해 얻은 특징값의 분포가 원하는 통계적 특성을 가지도록 변환행렬 최적화
( 주어진 데이터간 거리(유사도)가 추출된 저차원 특징들 사이에서도 유지되는데 관심 )
- 기본 목적 : 두 데이터쌍의 거리를 최대한 유지하는 방향으로 차원축소
데이터 집합 {𝑥₁,𝑥₂,...,𝑥ₙ}
추출된 저차원의 특징 { 𝑦₁, 𝑦₂, ... , 𝑦ₙ } , 𝑦ᵢ = 𝑓(𝑥ᵢ)
원 데이터의 거리행렬 D = { dᵢⱼ} , dᵢⱼ= dist(𝑥ᵢ , 𝑥ⱼ)
특징 벡터의 거리행렬 𝞓 = { 𝞭ᵢⱼ }, 𝞭ᵢⱼ = dist (𝑦ᵢ , 𝑦ⱼ)
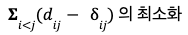
- 거리의 정의에 따라 다양한 방법의 존재
(1) 다차원 척도법 (MDS, Multi-Dimensional Scaling : MDS)
- 거리행렬 D가 값으로 정의되거나 유클리디안 거리 사용
dᵢⱼ = dist(𝑥ᵢ , 𝑥ⱼ) = || 𝑥ᵢ - 𝑥ⱼ|| ²으로, 𝚺ᵢⱼ( dᵢⱼ - 𝞭ᵢⱼ)²를 최소화하는 특징 { 𝑦₁, 𝑦₂, ... , 𝑦ₙ }를 찾음

(2) t-SNE (통계적 이웃 임베딩 : Stochastic Neighbor Embedding)
- 확률밀도함수를 활용하여 거리정의
- 데이터간의 거리와 특징간의 거리를 조건부 확률을 이용한 유사도로 정의
거리가 멀리 떨어진 데이터 사이의 관계를 더 잘 반영
- 확률분포와 KL-divergence로 정의되는 목적함수를 최소화하도록 반복적으로 y값들을 update

- 데이터가 정규분포를 따른다는 가정하의 유사도,
t-SNE에서는 특징벡터간 유사도는 분산이 1인 t분포를 따른다고 가정
( 기본 SNE 정규분포를 가정하여 정의함 )
** 일반적인 경우


(3) Isomap(측지거리 사용, geodesic distance )
- 유클리디안 거리보다 데이터의 분포를 반영한 거리를 반영하고자 함
데이터들을 정점으로 가지는 그래프간의 경로를 데이크스트라 알고리즘으로 계산
- 전체 거리에 대한 거리행렬이 얻어지면 MDS등을 이용해 저차원 특징값을 찾을수 있음

(4) 거리기반 차원축소 방법의 특징 (선형변환과 비교하였을때)
① 입력데이터와 특징데이터간의 매핑함수를 정의하지 않음 (다양한 방법 사용)
특히 MDS에서는 입력좌표값이 따로 주어지지않고 거리값만 주여져도 적용가능
② 저차원에 특징값에 대한 목적함수가 정의되고 최적화 과정을 거침
- 선형변환이 변환행렬 W를 찾으나 거리기반 차원축소는 현재의 데이터 특징을 잘 표현하고자 함 )
- 새로운 데이터에 대해서는 대응되는 특징값을 찾을수 없음(PCA, LDA처럼 주어진 새로운 문제 해결X)
③ 데이터 시각화의 용도로 주로 사용 (데이터의 값보다 데이터간 상호관계, 유사도-거리등에 의미를 둠)
'스터디 > Machine Learn' 카테고리의 다른 글
| 6. Deep Learning (0) | 2024.08.28 |
|---|---|
| 5. 신경망 (0) | 2024.08.27 |
| 4. 앙상블, 결정트리, 랜덤포레스트, SVM/커널 (0) | 2024.08.20 |
| 2. 지도학습- 분류와 회귀 (0) | 2024.08.01 |
| 1. 머신런 개요 _ 행렬연산 (0) | 2024.06.09 |