Graph

1. 용어
(1) 그래프는 vertex와 edge로 구성 G = (V, E)
(2) 변은 두 꼭지점을 연결(두 꼭지점은 변에 의해 발생)
(3) 연결된 꼭지점은 서로 인접
(4) 병렬변 두 꼭지점을 연결하는 변이 복수개
(5) 루프 동일한 꼭지점을 연결한 변
(6) 고립된 꼭지점 어떤 변도 연결되지 않은 꼭지점

(7) 차수 G의 총차수 (모든 꼭지점의 차수의 합 ), v의 차수 (인접한 변의 갯수)
(8) Handshaking Lemma 그래프의 총차수는 짝수 (변은 반드시 두개의 끝점)

2. 그래프의 종류
(1) 방향그래프는 변이 방향을 가지며, 무향그래프는 방향이 없음
(2) 단순그래프는 루프가 없고, 병렬변을 가지지 않는 그래프 (반대: 다중그래프)
(3) 부분 그래프 그래프의 일부분
(4) 부분 신장그래프 모든 vertex를 지나는 부분 그래프 (최소신장그래프 : 가중치가 가장작은 신장그래프)

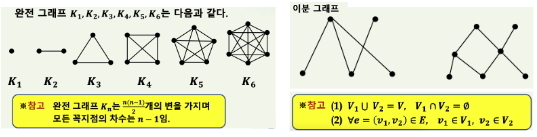
(5)Complete Graph (완전 그래프)
G = (V, E) ∀u ,∀v∈ V, ヨe = (u,v) ∈ E, G는 완전 그래프
Kₙ : |V| = n인 완전 그래프, 임의의 두 꼭지점을 연결하는 변이 항상 존재하는 그래프
(6) Bipartite Graph(이분 그래프)
G = (V, E), V는 연결성분 V₁, V₂로 분할되어 있고 모든 변들이 V₁의 꼭지점과 V₂의 꼭지점을 인접시키는 경우
(7)완전이분그래프

(7)k-정규그래프

3. 그래프의 표현
(1) 발생행렬 (incidence matrix)
G(V,E) 꼭지점을 행으로 변을 열로 하여 변과 꼭지점 사이의 발생관계를 표현한 행렬

(2) 인접행렬 (adjacency matrix)
G(V,E) 꼭지점을 행으로 변을 열로 하여 꼭지점과 꼭지점 사이의 발생관계를 표현한 행렬

(3) 연결리스트 (adjacency list)
G(V,E) 각 꼭지점에 인접하는 꼭지접들을 차례로 연결 리스트로 표현한 것

4. 그래프의 탐색 (visit)
(1) walk (워크)
G(V,E), V₀ , Vₖ ∈ V,
V₀ (시작점) 에서 시작하여 Vₖ(종점)에 도착하는 꼭지점과 변들을 나열, V₀ = Vₖ 는 닫혀있음
(2) trail (트레일)
워크의 변들이 모두 서로 다르면 w는 트레일
워크의 꼭지점들이 모두 서로 다르면 w는 경로

(3) trail (트레일)
w가 트레일이고 V₀ = Vₖ 이면 닫힌 트레일
사이클 (cycle) w가 경로이고 V₀ = Vₖ 이면 닫힌 경로로서 길이가 k인 k-사이클

(4) cycle (사이클)
G(V,E), (u,v) ∈ V
u에서 v로 가는 경로가 존재하면 u와 v는 연결
v의 꼭지점은 연결, 다른 집합과 겹치지 않는 꼭지점의 집합
➯ V₀,V₁, V₂, V₃,..., Vₙ 은 G의 연결성분
➯ ∀u ∈ V,∀v∈ V, u에서 v로 가는 경로가 존재하면 G는 연결그래프
➯ G는 하나의 연결성분으로 구성

(5) 평면그래프와 4색정리
▷ 평면그래프 그래프의 모든변을 서로 교차하지 않게 그릴수 있는 그래프

▷ 오일러의 공식과 4색정리
v - e + f = 2 , 면(face)은 연결된 평면 그래프에서 변들로 만들어지는 사이클을 경계로 형성된 공간

(5) 오일러 투어
▷ 오일러 트레일 그래프의 모든 변들을 한번만 지나는 트레일
▷ 오일러 투어 닫힌 오일러 트레일 (닫힌 오일러 트레일, 시작점과 종점이 같은 오일러 트레일)
▷ 오일러 그래프 오일러 투어를 갖는 그래프 (모든 꼭지점의 차수는 짝수)
▷ 오일러 투어 (알고리즘)
G의 임의의 꼭지점 v, v에서 시작하고 v에서 끝나는 임의의 사이클 C,
C가 오일러 투어이면 증명 완료, G에서 C에 속하는 모든 변을 제거하고 새로운 G'
C와 G'공유하는 꼭지점 중 하나를 w라고 두고 w시작 w완료인 임의의 사이클 C'
C와 C'를 합하여 새로운 C

(6) 해밀턴 경로
▷ 해밀턴 경로 그래프의 모든 꼭지점을 한번씩만 지나는 경로
▷ 해밀턴 사이클 닫힌 해밀턴 경로 (시작점과 종점이 같은 해밀턴 경로)

5. 그래프의 활용
(1) 가중 그래프 (weighted graph)
그래프의 각변에 실수값이 붙여진 그래프, 변에 부여된 값은 가중치(weight)라고 함
▷ 최단경로문제 출발지와 도착지가 주어졌을때 가장 짧은 경로를 찾는 문제
▷ 최소신장트리문제 그래프의 모든 꼭지점을 최소수의 변으로 연결하는 문제 (가중그래프를 이용)

'스터디 > 이산수학' 카테고리의 다른 글
| 이산수학 - 조합이론 (2) | 2023.06.11 |
|---|---|
| 이산수학 - Tree (1) | 2023.06.11 |
| 이산수학 - 함수 부울대수 (0) | 2023.06.11 |
| 이산수학 - 집합 행렬 관계 (1) | 2023.06.11 |
| 이산수학 - 논리와 증명 (0) | 2023.06.10 |