검사 프로시저 개선(우수한 수만 인식)
경로상에 존재하는 수를 일정한 깊이만큼 내다보고 평가함수를 이용하여 점수를 부여
- 몬테카를로 탐색은 평가함수를 설정하기 어려운 경우에 사용
- 최대최소탐색은 나에게 유리한 조건으로 평가함수를 설정하여 조건별 탐색
1. 최대 최소탐색 (minimax search)
1) 최대최소탐색에 의한 수의 선택
- 현재 상태를 루트노드로 최대화와 최소화로 다음 수들의 가치평가, 유리한 수 선택
( 나와 상대방이 서로에게 최적의 선택을 한다는 가정하에 가치가 최대가 되는결정)
- 상대방과의 대결에서 승리하기 위한 게임
최대화 : 내 차례에서 내가 둘수 있는 수 중에서 가장 유리한 수를 선택
최소화 : 상대방은 자신이 둘수 있는 수중에서 나에게 가장 불리한 수를 둘것이라고 가정함


2) 탐색의 진행
트리의 규모가 크면 모든 경우 탐색으로 종단 (게임을 진행불가, 승리/패배/무승부가 결정)에 도달불가
시스템의 가용 자원에 따라 깊이 탐색을 결정 (정해진 깊이 도달시 경험적 지식을 반영하여 설계된
함수를 통해 노드의 가치를 추정)
평가함수 : 판의 형태가 나에게 얼마나 유리한가(이길 가능성)를 예측하도록 설정
- 삼목게임 ( 두 사람이 가로/세로 3X3 크기의 판에 교대로 수를 두어 행,대각선,열을 점유하면 승리
평가함수의 정의 F ( W: 이길 가능성의 행, 열, 대각선 수), ( L : 질 가능성의 행, 열, 대각선수)
승리 : F = ∞ , 패배 : F = -∞ , 그외의 경우 F = W - L

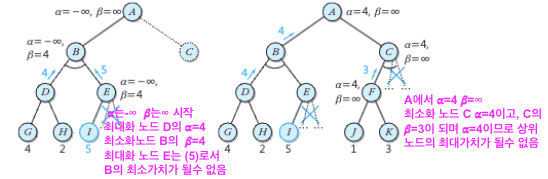
3) 𝛂 - 𝜷 가지치기
최대최소 탐색트리에서 탐색이 불필요한 가지가 많이 발생하므로, 불필요한 가지를 잘라
탐색의 성능을 높이기 위한 알고리즘 (조건으로 받은 𝛂, 𝜷를 감안하여 가지치기)
① 𝛂 : 어떠한 최대화 노드의 최대화 과정에서 지금까지 구한 가장 큰 가치
가치를 구하려는 후계노드(최소화 노드)보다 더 큰 가치를 가져야 함
( 최소화 노드, 후계노드의 가치가 𝛎일때 𝛂 ≥ 𝛎 라면 그 최소화노드의 나머지 후계는 가지치기 )
② 𝜷 : 어떠한 최소화 노드의 최소화 과정에서 지금까지 구한 가장작은 가치
가치를 구하려는 후계노드(최대화 노드)보다 더 작은 가치를 가져야 함
( 최대화 노드, 후계노드의 가치가 𝛎일때 𝜷 ≤ 𝛎 라면 그 최소화노드의 나머지 후계는 가지치기 )

𝛂 - 𝜷 가지치기의 예

2. 몬테카를로 트리 탐색 (Monte Carlo tree search : NCTS)
게임과 같은 의사결정 문제에 활용되는 경험적 탐색 알고리즘
- 노드 선택전략은 UCT, 시뮬레이션 전략은 무작위 선택 & 역전파
방대한 수가 경우의 수가 있는 게임에서 경험적 지식을 이용한 평가함수 설정이 어려움
→ 탐색공간의 무작위 표본화를 바탕으로 탐색트리 구성 (점증적 비대칭적 트리, 탐사와 활용의 균형중요)
루트노드에서 적절한 자식노드를 선택과정을 반복, 리프노드에 도달한 후 자식노드를 생성하여 트리를 확장
→ 새로 생성된 노드의 가치 파악 (시뮬레이션, 몬테카를로 롤아웃, 리프노드부터 루트노드까지 통계치 업데이트)
→ 미리 정의된 계산 예산(시간, 메모리, 반복등의 조건)에 도달할때까지 반복
→ 가장 적절한 행동을 선택
1) 탐색 알고리즘
① 선택(selection) : 루트노드로부터 선택전략에 따라 자식노드를 선택하는 과정을 깊이방향으로 반복
( 시도해보지 않은 방향이 남아있는 노드에 도달할때까지 반복)
② 확장(expansion): 선택된 노드에 새로운 행동을 함으로써 자식노드를 생성하고 트리를 추가하여 확장
③ 시뮬레이션(simulation) : 확장된 노드로부터 게임이 끝날때까지 스스로 게임진행(롤아웃, 플레이아웃)
④ 역전파 (backpropagation): 시뮬레이션 결과를 확장된 노드로부터 루트노드까지 선택경로를 따라 역전파(통계 업데이트)


2) 탐색
①선택전략
주어진 노드의 자식노드 중 하나를 선택하기 위한 전략, 탐사와 활용사이의 균형 이루도록 설계
탐사: 평가의 불확실성으로 인해 아직은 덜 유망하나 향후 우수한 것으로 드러날 수 있는 수를
선택할 수 있도록 하는것
활용 : 지금까지의 결과중 가장 우수한 결과를 이끌어내는 수를 선택
Multi-armed bandit(MAB)문제 (카지노의 레버가 여러 개인 슬롯머신)와 관련하여
UCT(upper confidence bound applied to trees) 알고리즘으로 연구
- UCB1 : 잘 알려진 신뢰도 상한 (upper confidence bound : UCB)
노드 nₚ에서 자식 노드들 중 하나를 선택할 때 자식노드 nᵢ의 UCB1을 계산
(지금까지 알고 있던 평균가치(활용)와 방문횟수(탐사)에서 C(상수)를 이용하여 적절히 균형
부모노드의 방문횟수가 많고 해당 노드 방문횟수가 적으면 탐사가 큰 비중)

②시뮬레이션 전략
선택된 노드로부터 게임이 끝날대까지 스스로 수를 선택하여 게임을 진행
수의 선택방법 - 순수한 무작위 방법 (매우 많은 시도가 필요)
적절한 시뮬레이션 전략에 따른 유사 무작위 수 (시도횟수를 줄일수 있음)
③ 역전파 전략
가치의 누적값과 방문횟수를 각각의 노드에 저장하고, 이의 평균을 사용하는 방법
④ 최종 최적행동 선택
적절히 정한 계산 한계에 도달하여 시뮬레이션을 마치고, 자식노드중에 하나를 선택하는 전략
최대자식 (max child) : 가장 큰 보상을 갖는 자식선택
강인한 자식(robust child) : 가장 많이 방문한(선택된) 자식을 선택 ( ▶ 알파고에 활용한 방법 )
최대-강인자식(max-robust child) : 방문횟수가 많고 가장 큰 보상을 갖는 루트의 자식을 선택
안전한 자식(secure child) : 신뢰도 하한(lower confidence bound)이 최대인 자식을 선택


** alphaGo Fan의 개요 (몬테카를로 트리탐색 수행)
탐색의 각 단계에 필요한 결정을 위해 프로기사 기보와 자가대결을 위해 학습된 신경망 활용
바둑반 돌배치를 19*19 영상의 형태로 전달하고, CNN으로 학습/분류/회귀등의 처리수행
가치망을 이용하여 착점의 가치를 평가, 정책망을 이용해 착점을 샘플링하거나 탐색진행방향결정
AlphagoLee(이세돌대결), AlphaGoMaster, AlphaGoZero, AlphaGoZero(기보없이 혼자 학습), AlphaZero(바둑외의 게임, 체스등)
