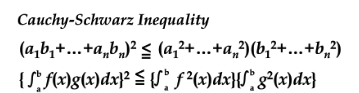행렬의 대각화

 

1. 대각행렬

 

 

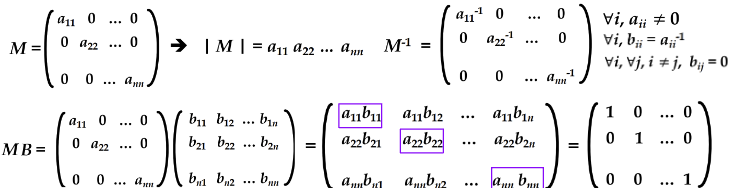
(1) 대각행렬의 고유값

| M - λI | = 0 

 

(2) 대각행렬의 거듭제곱(멱승)

 

(3) 행렬의 대각화 가능성

M, N : n차 정방행렬, D: 대각행렬

MP = PN , M = PNP⁻¹( N : eigenvalue matrix )

 

N= PMP⁻¹를 만족하는 P가 존재, M과 N은 유사(similar) 상사행렬

N= PMP⁻¹  ↔ N= P⁻¹MP  

M과 D가 유사하다. 즉 M=PDP⁻¹ ↔ M이 대각화 가능하다. (diagonalizable)

 

 

대각화 불가능

 

(4) 행렬의 대각화

M의 고유값 λ₁,λ₂,..,λₙ에 각각 대응하는 M의 고유벡터 A₁,A₂,...,Aₙ이 서로 일차독립이면

정칙행렬 P, 대각행렬 D가 존재하여 M=PDP⁻¹을 만족하며, 

n차 정방행렬 M이 서로 일차독립인 n개의 고유벡터를 가지면, 대각화 가능( ∃D,∃P, M=PDP⁻¹) 

 

▷ n차 정방행렬 M이 n개의 서로 다른 고유값을 가지면 대각화가능

   (n개의 고유값을 가지면 서로 일차독립인 n개의 고유벡터를 가짐)

    n차 정방행렬 M이 대각화가능하면 n개의 서로 다른 고유값을 가짐 

 

(5) 피보나치 수열 (Fibonacci sequence)

a₀ = a₁ =1, aₙ = aₙ₋₁ + aₙ₋₂

 

행렬 대각화 응용 , Aₙ = Mⁿ⁻¹A₁ 

M이 대각화 가능한가? 고유값, 고유벡터구함 , 행렬 P,D구함, 일반항 aₙ

 

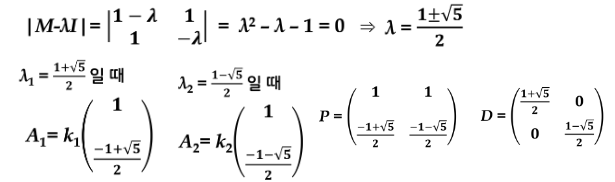
(6) 일반항 

Aₙ = Mⁿ⁻¹A₁ 은 Aₙ = PDⁿ⁻¹P⁻¹A₁ 

 

2. 일반벡터공간에서의 내적 

벡터공간 V의 임의의 두 벡터 A,B에 대해 실수 <A,B>를 대응시키는 관계가

다음을 만족할때, <A,B>를 A와 B의 내적

< , > : 벡터공간 V에 정의된 내적 (V를 내적공간으로 표시), {V, < ,>}로 표시함 

A, B, C ∈ V, k ∈ R (실수집합)

① < A,B > = < B, A >

② <A, B+C> = < A,B > + < A,C >

③ < kA, B > = k (A,B)

④ <A,A> ≥ 0 이고, <A,A>=0 일 필요충분 조건은 A=0

※ Rⁿ벡터공간은 내적공간으로서 {Rⁿ,· }로 표시됨

※ 일반벡터의 연산은 < ,> 이고 Rⁿ벡터는 · 

 

(1) 일반내적공간{V, < ,>}의 벡터크기 

||A|| = √<A,A>

 

Schwarz부등식

내적공간 {V, < ,>}에서 임의의 벡터 A,B ∈  V에 대해 |<A,B>| ≤ ||A|| ||B||

O벡터가 아닌 A,B에 대해 

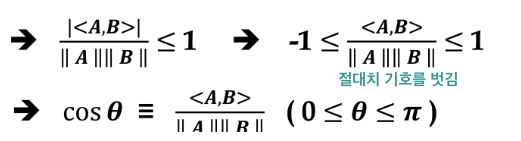
( <A,B> = cos 90˚ = 0, orthogonal 직교 )

 

 

(2) 직교벡터들의 일차독립성

내적공간{V, < ,>}에서 벡터 A₁, A₂,...,Aₙ(단, Aᵢ ≠ Ø)이 서로 직교하면 이 벡터들은 일차독립

 

직교집합 : 서로 직교인 O이 아닌 벡터[직교벡터]들의 집합 (내적하면 0)

단위직교집합 : 길이가 1인 직교벡터들의 집합

정규화과정 (normalization) 

 

직교보공간 

내적공간{V, < ,>}에서 벡터 A가 V의 부분공간 U의 모든 벡터들과 직교하면, 

벡터 A는 U와 직교한다. U와 직교하는 V의 모든 벡터들의 집합을 U의 직교보공간

(부분공간에 대해 직교하는 모든 A의 집합)

 

 

내적공간{V, < ,>}에서 U를 V의 부분공간이라고 하면, 

 

(3) 직교행렬

 

직교행렬인지 확인하려면 역행렬을 구해서 전치행렬과 동일한지 확인 

 

 

(4) 직교행렬의 행렬식 

M이 직교행렬 , 행렬식은 1 또는 -1

 

 

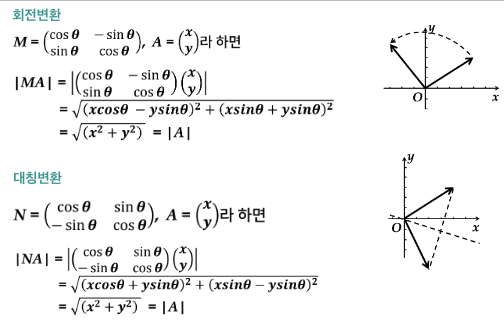
(5) 2차 직교행렬의 특성

2차 정방행렬 M이 직교행렬이면, M은 회전변환 또는 대칭변환에 대응하는 행렬

 

대칭행렬 M은 직교행렬에 의해 대각화된다. 

 

(6) 직교변환

▷ R² 공간의 직교행렬

2차 직교행렬 ≫ 회전변환 또는 대칭변환 , 길이가 변하지 않음

 

▷ 직교변환

내적공간{V, < ,>}, {W,<,>}: 내적 공간일때 

T: V → W : 선형변환,  || T(A) || = || A ||이면 T를 직교변환(orthogonal transformation)

아래는 모두 동치

① T가 직교변환  (벡터의 길이가 보존)

② ∀A,B ∈ V, <A,B> = <T(A), T(B)>   (내적이 보존)

③ 내적공간 V의 단위직교기저 {Aᵢ}에 대해 {T(Aᵢ)}는 내적공간 W의 단위직교집합 (각도보존)

④  단위직교기저에 의한 T에 대응하는 행렬 M, dim V=dim W=n 이면 M은 n차 직교행렬 

 

▷ 직교변환과 직교행렬

 

 

 

3. 직교기저

 

 

{ Rᣕ, · }의 경우 

 

 

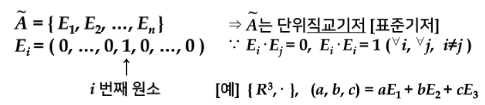
벡터의 이차결합표현

 

 

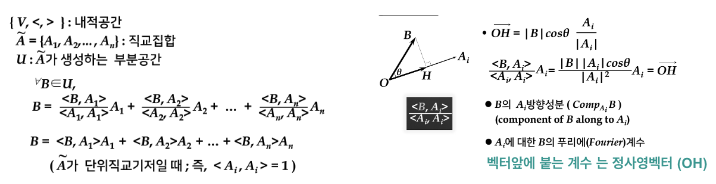
일반 내적공간에서는 (직교기저)

 

 

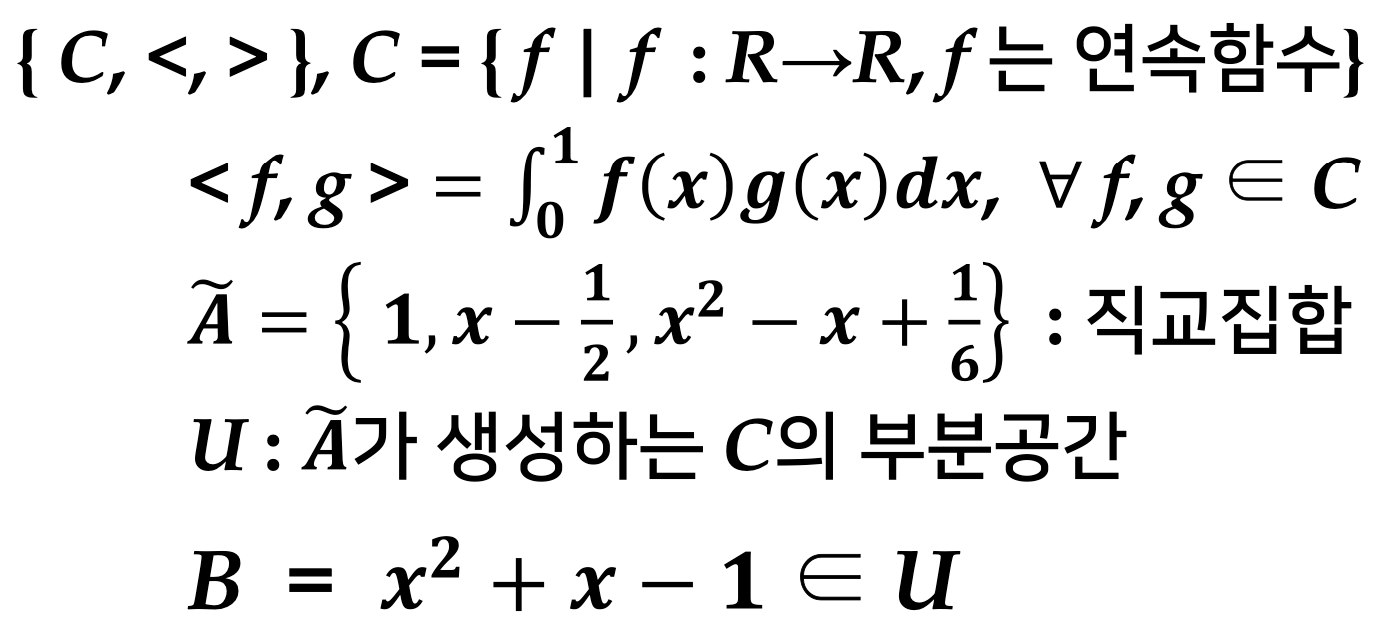
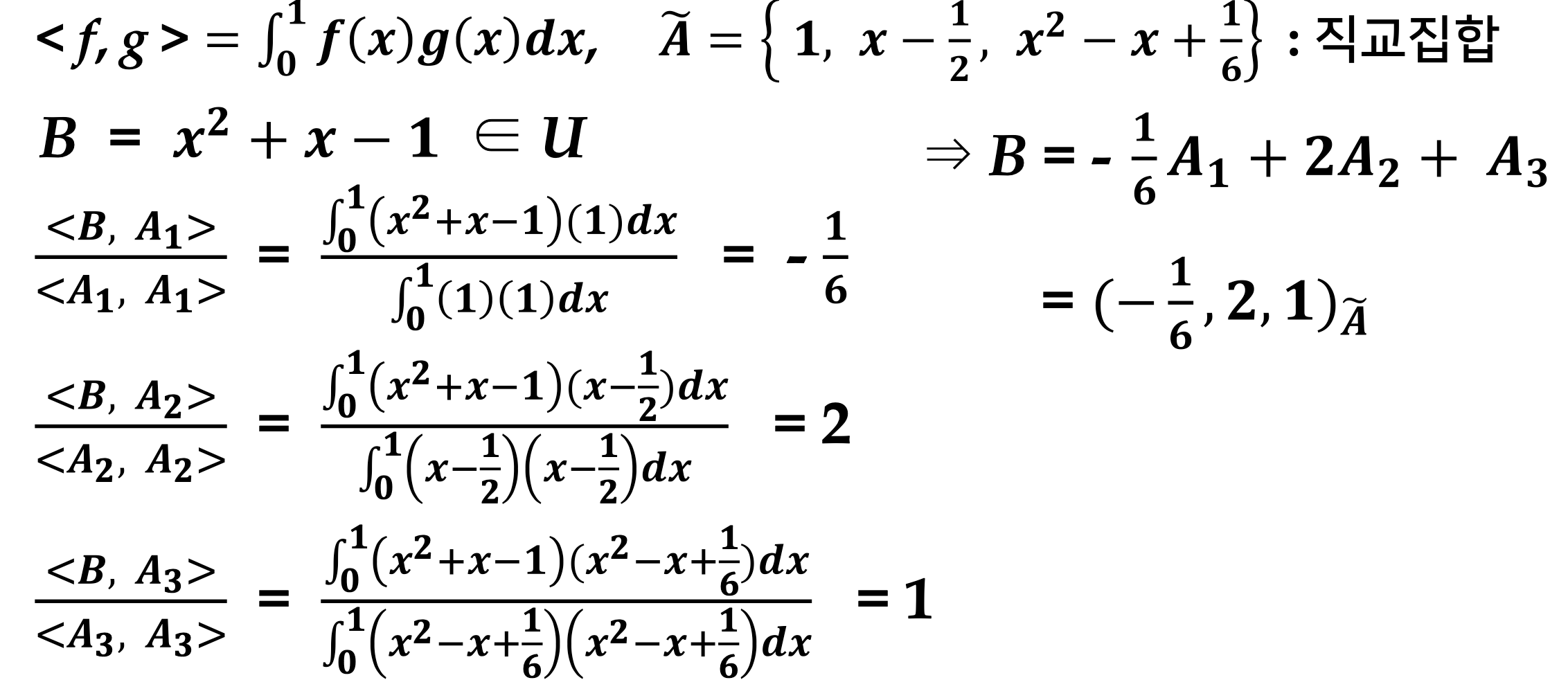
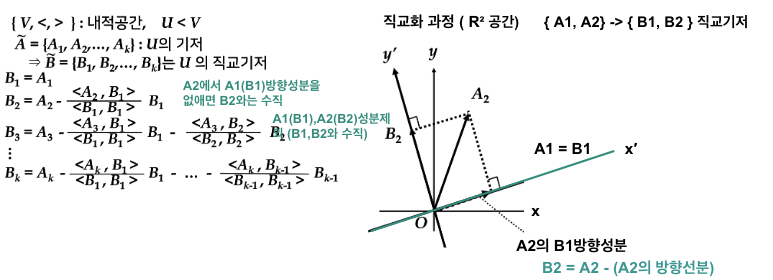
그램 - 슈미트 직교화

 

 

단위직교기저

내적공간{V, < ,>}의 부분공간 U는 단위직교기저를 정규화

( Bᵢ / ||B|| )

 

 

정사영벡터와 직합

벡터 A의 부분 공간 W로의 정사영벡터 

 

정사영벡터

 

 

최소자승법 (least square solution, curve fitting을 위해 사용)

 

_______________________________________________________

※ 참조