Heap
힙 추상자료형
피라미드 모양으로 쌓아올린 더미, 가장 위에 있는것을 우선 꺼내는 구조
부모-자식 사이(부분적으로) 정렬된 완전이진트리로, 부모노드의 우선순위가 높음
힙의 연산
① insert(element) 힙에 데이터 삽입
② delete() 힙(루트)에서 데이터 삭제
③ peek() 힙(루트)에서 데이터 읽어오기
④ isEmpty() 힙이 비어있는지 확인
⑤ size() 힙에 저장한 데이터 갯수확인
최소힙
루트가 전체노드중에서 최소값이며 부모노드가 자식노드보다 작은 값을 가짐
트리의 레벨에 따른 데이터 순서가 없으며, 왼쪽 노드와 오른쪽 노드사이 크기제한 없음
최대힙
루트가 전체노드중에서 최대값이며 부모노드가 자식노드보다 큰값을 가짐
트리의 레벨에 따른 데이터 순서가 없으며, 왼쪽 노드와 오른쪽 노드사이 크기제한 없음

우선순위 큐: 대기리스트에 우선순위가 높은 사람이 먼저 서비스를 받는 구조
ex) 데이터 삭제와 삽입 시 특정순위(가장 작은값, 혹은 가장 큰값)이 삭제
(Delete_q(), Add_q(3))
Delete_q()에 의해 큐의 front의 1이 삭제되고, 나머지 데이터중 가장 작은 데이터가 다음 삭제위치로 이동하고 rear가 바뀜

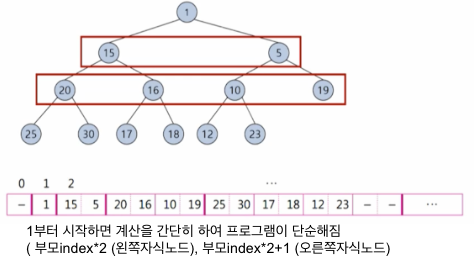
배열을 이용한 힙의 구현
완전이진트리이기 때문에 배열로 구현해도 기억장소의 낭비가 없음
연결리스트보다 실행속도면에서 효율적, 메모리 효율측면에서도 장점
힙의 노드삭제 (힙은 루트에서만 삭제)
- 루트 삭제후, 맨뒷편의 리프노드의 값을 루트노드 이동
- 자식노드와 비교하여 작은 값과 위치교환 ( 트리의 리프노드까지 반복수행)

▶ 힙의 구조
typedef struct heap {
int heap[MAX_SIZE]
int size;
} heap;
▶ 힙의 노드삭제
int min_heapDelete(heap *h) {
int parent, child;
int data, temp;
data = h → heap[1]; // 루트 노드의 값
temp = h → heap[(h→size)--]; // 마지막 값
parent = 1;
child = 2;
while(child <= h → size) { // 전체 배열의 크기를 벗어나지 않도록 제어
if((child < h → size )&& (h→ heap[child] > h→ heap[child+1])){
child ++; } // 왼쪽은 child, 오른쪽은 child+1
if(( temp <= heap[child]) // 맨뒤의 루트노드가 child보다 작은지 체크
break; }
h → heap[parent] = h → heap[child]; // 루트에 자식노드의 작은값 교체
parent = child ; // 현재의 자식노드를 다음 순차의 부모노드로
child *= 2; // 현재의 자식노드의 자식노드를 다음순차의 자식노드로
}
h → heap[parent] = temp;
return data;
}
▶ 힙의 노드삽입
void min_heapInsert(heap *h, int data) {
int i;
i = ++ ( h→ size ) ;
while( i != 1 ) && ( data < h → heap([i/2]) { //i가 정수여서 내림한 정수가 결과임
h → heap[i] = h → heap[i/2]
i /= 2;
}
h → heap[i] = data;
}
